La estadística nos proporciona herramientas para analizar y comparar nuestros datos con funciones probabilísticas teóricas que nos facilitan la toma decisiones. En el análisis de grafos se necesitan también de instrumentos para estudiar las propiedades de los grafos encontrados en el mundo real. Para ello, necesitamos definir grafos realistas para evaluar aspectos claves de los grafos como el diámetro, el coeficiente de agrupación o la distribución de grado. Los grafos creados para tal propósito son grafos aleatorios, construidos a partir de un modelo.
En este post se tratan tres modelos de grafos aleatorios como son:
- Modelo Erdös-Rényi
- Modelo Watts-Strogatz
- Modelo Barabasi-Albert
Modelo Erdös-Rényi
El modelo de Erdös-Rényi es un grafo aleatorio con \(N\) vértices y \(M\) aristas que se asignan con probabilidad \(p\) de manera independiente. Cualquier topología generada en la red es igual de probable.
Para estimar la probabilidad \(p\) de que una pareja de nodos estén conectas se divide el número de aristas \(M\) por el número total de posibles parejas\(M_{p}\) de manera:
\[p = \frac{M}{M_{p}}\]
Recordemos que el número total de aristas se define como: \(M_{p} = \binom{n}{2} = \frac{n(n-1)}{2}\) siendo N el número de vértices en el grafo.
Alguna de las propiedades este modelo son:
- El diámetro de es de orden \(O\left ( log N \right )\)
- El grado promedio de un nodo es \(p(n-1)\). El grado máximo de un nodo es \((n-1)\) y \(p\) es la probabilidad la presencia de la arista. Lo mas relevante de la distribución del grado es que sigue una distribución Poisson , y queda lejos de las distribución de ley de potencias típicas en las redes sociales.
- El coeficiente de clustering en el modelo de Erdös-Rényi es un valor muy próximo al valor \(p\).
Implementación del modelo Erdös-Rényi en R
El modelo Erdös-Rényi esta incluido en el paquete igraph. El siguiente trozo de código muestra un ejemplo para generar una red de 50 nodos y 100 aristas.
# Dependencias
require(igraph)
require(ggraph)
# Creación del grafo
set.seed(42)
erdos <- erdos.renyi.game(50, 100,"gnm")
ggraph(erdos, layout = 'fr') +
geom_node_point(size = 2.5) +
geom_edge_fan(aes(alpha = ..index..), show.legend = FALSE) +
theme_graph()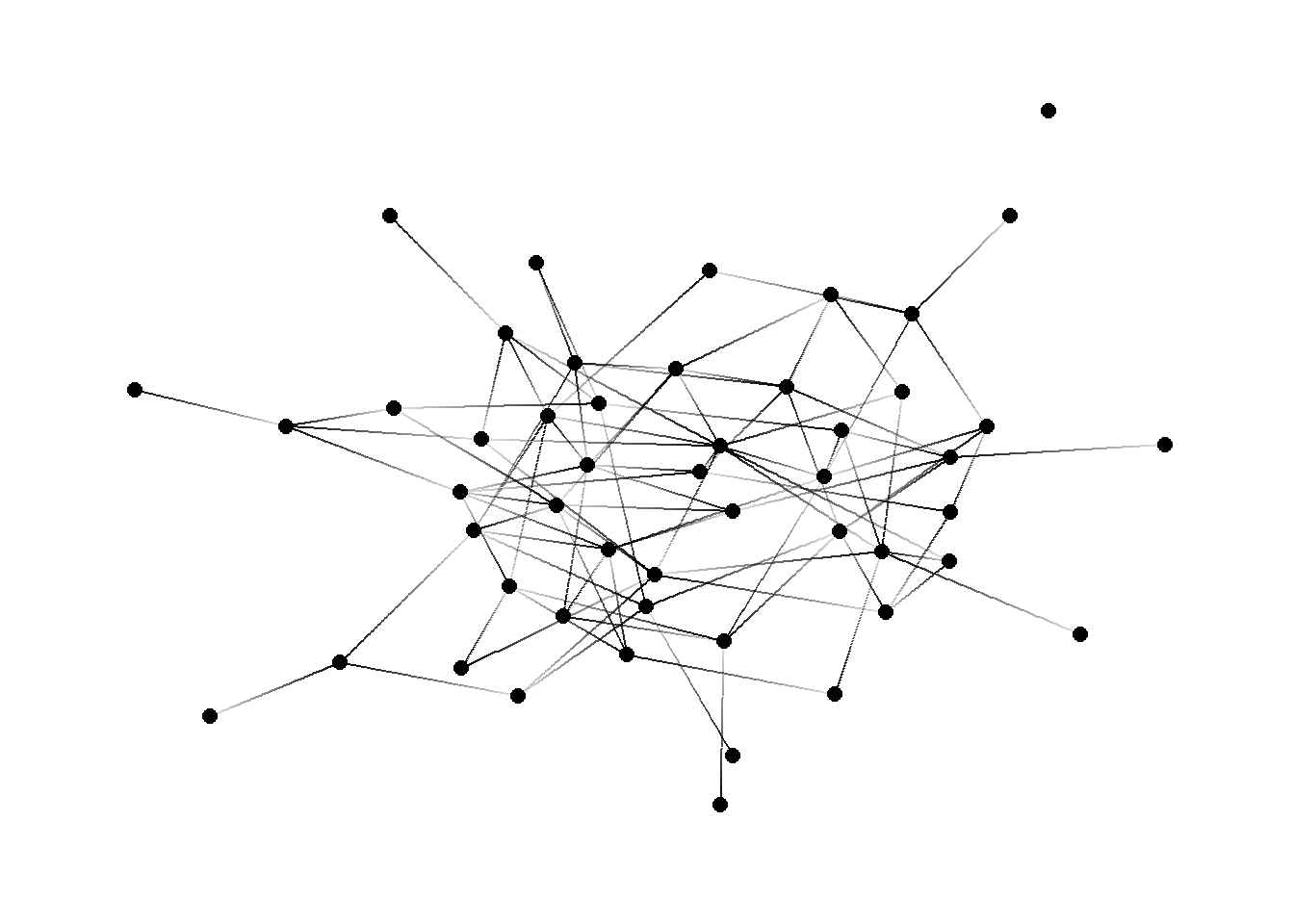
Figura 1: Grafo Erdös-Rényi con 50 vértices y 100 arístas
Modelo Barabasi-Albert
El modelo Barabasi-Albert genera las aristas a partir del grado de los nodos. A mayor grado del nodo mas probable es que genere una nueva arista en ese nodo. Este sistema se conoce como conexión preferencial (preferential attachments) y se puede explicar con la paradoja de “the rich get richer”.
Los nodos se añaden a la red de manera secuencial utilizando la probabilidad \(p_{i}\) de que un nuevo nodo se conecte con \(i\), concretamente:
\[p_{i} = \frac{ k_{i} } { \sum_{j} k_{j} }\]
donde \(k_{i}\) is el grado del nodo \(i\) y la suma se realiza sobre todo los existentes nodos \(j\). El denominaodor se puede ver como el doble de aristas en la red.
Como propiedades principales podemos destacar:
- El diámetro en este modelo es \(O(log \: log N)\). Estos valores son más pequeños que el modelo de Erdös-Rényi, ya que los nodos tienden a concentrase en hubs.
- La distribución de grado y el coeficiente de clustering se ajustan a una ley de potencias.
Implementación del modelo Barabasi-Albert en R
Al igual que el modelo anterior el modelo Barbasi-Albert se puede generar en R. A continuación se muestra un ejemplo:
# Dependencias
require(igraph)
require(ggraph)
# Creción del grafo
set.seed(42)
barbasi <- sample_pa(50, power = 2, directed = FALSE)
# Nota: El factor de conexión preferencial es dos para hacer mas
# visible su efecto.
ggraph(barbasi, layout = 'fr') +
geom_node_point(size = 2.5) +
geom_edge_fan(aes(alpha = ..index..), show.legend = FALSE) +
theme_graph()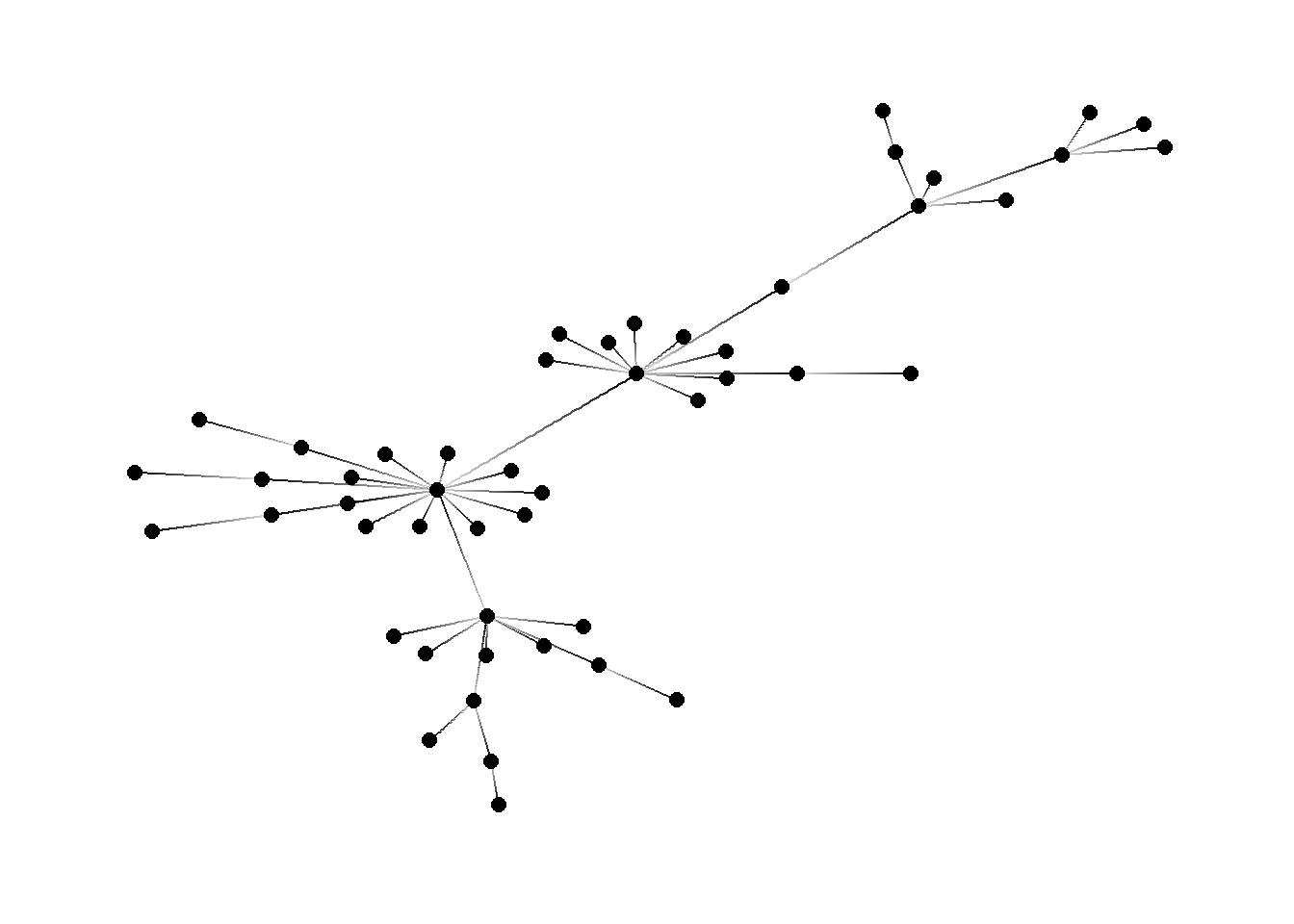
Figura 2: Grafo basado el modelo Barbasi-Albert con 50 vértices
Modelo Watts-Strogatz
El modelo presentado por Watts y Strogatz parte de un grafo con \(N\) nodos donde estos nodos se conectan a sus dos vecinos mas cercanos describiendo una forma de anillo. Esta red en forma de anilla tiene un coeficiente de clustering alto pero también el diámetro del grafo los es.
Por cada arista con probabilidad \(p\) se evalúa la conexión y se cambia por cualquier otro nodo. Si \(p=0\) el anillo inicial se queda intacto, sin embargo si \(p=1\) los cambios de aristas generan desorden en la red.
Sus propiedades principales son:
- El diámetro es alto si \(p\) es próximo a 0. Si \(p\) es próximo a 1, la red se asemeja a una red Erdös-Rényi.
- La distribución de grado cuando \(p\) es próximo a 0 se asemeja a una función Delta de Dirac. Cuando \(p\) es próximo a 1, la distribución la podemos relacionar a una distribución de Poisson.
- El coeficiente de clustering es alto para valores de \(p\) próximos a 0. No obstante, el valor de clustering tiende a ser bajo a medida que \(p\) aumenta.
Implementación del modelo Watts-Strogatz en R
Al igual que los modelos anteriores, este modelo también se puede generar en R. A continuación se muestra un ejemplo:
# Dependencias
require(igraph)
require(ggraph)
# Creción del grafo
set.seed(42)
watts <- sample_smallworld(1, 50, 1, 0.15)
ggraph(watts, layout = 'circle') +
geom_node_point(size = 2.5) +
geom_edge_fan(aes(alpha = ..index..), show.legend = FALSE) +
theme_graph()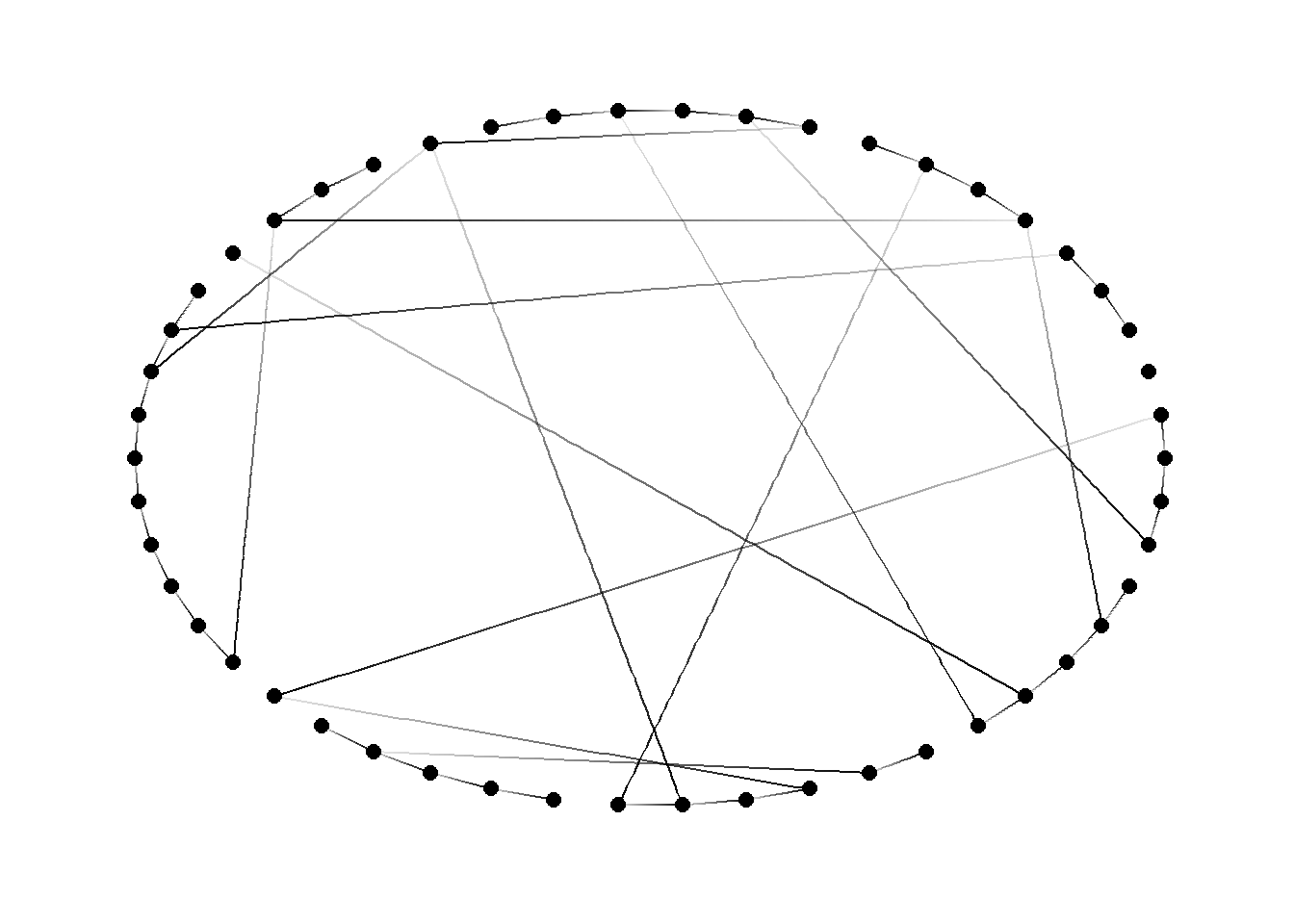
Figura 3: Grafo basado el modelo Watts-Strogatz con 50 vértices con probabilidad p = 0,15